Have you taken a walk through the rain on a warm spring day and seen that perfect pond? You know, the one where the raindrops seem to condense down at the right speed, causing ever-increasing circles?
Even before I entered the field of fluid flow research almost 15 years ago, I was interested in the waves that develop after a raindrop hits a pond.
As I focused on studying unstable waves in liquid sheets – aimed at dampening unwanted waves in industrial coating and atomization processes – my interest in pond waves turned into an obsession. What’s going on? Where does the pattern come from? Why does the impact of rain in a pond look different than rain falling elsewhere, such as in a lake or ocean?
It turns out that it’s all to do with something called a spread.
In the context of water waves, dispersion is the ability of waves of different wavelengths to each move at their own individual speeds. Looking down on a pond, we see a collection of such waves moving together as one ripple in the water.
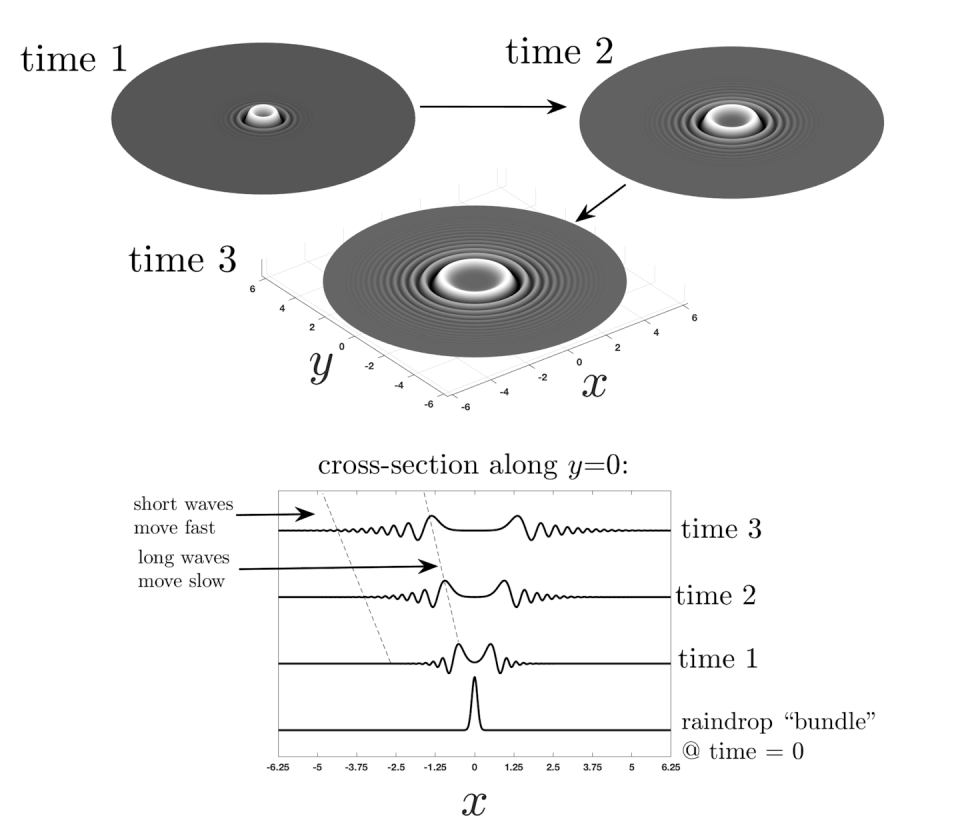
When a raindrop hits, imagine it as a “wedge” on the surface of the water. This wedge can be idealized as a wave packet of all sizes. When the raindrops fall, the packet waves are ready to start their new life in the pond.
However, whether we see those waves as ripples depends on the body of water the raindrop lands on. The number and spacing of the rings you see depends on the height of the pond. This was verified in some very cool ripple tank experiments, where drops of the same velocity fall into a container of water at different depths.
Shallow ponds enable ripples, because they are much thinner than they are wide. The balance between the surface force – between the pool of water and the air above it – and the gravitational force tips in favor of the surface force. This is crucial, since the surface force depends on the curvature of the water surface, but the gravitational force does not.
A puddle that is still shallow at first becomes curved on the surface after the raindrop hits. The surface force is different for long waves than for short waves, causing waves of different sizes to separate into ripples. For shallow ponds, the long waves move slowly from the point of impact, and the short waves move fast, and the short waves move really fast, becoming tightly packed at the periphery. This creates the enchanting pattern we see.
Raindrops may react differently in other situations. Imagine rain hitting a lake or ocean – or those deep puddles that need galoshes. Here, the raindrop hits the water, but the force due to gravity becomes more important. It moves waves of all sizes at the same speed which could overpower the rippling effect due to the force of the surface.
The combination of teaching undergraduate partial differential equations while continuing to research liquid sheets resulted in what I called the “pond equation”. When solved, the equation creates an animated simulation of what happens when a raindrop hits a pond. It is a simplified version of an equation in one of our group’s latest research efforts, but it is also consistent with the classical description of ripples.
I use this close-up description of pond waves as one way to get students excited about math by connecting it to the world around them.
The study of surface-driven waves is important for applications such as coating processes involved in making batteries and solar cells.
Such waves are also seen as a result of the foot stroke of water striders, but research has found that the water strider is not specifically looking to make these waves to enable travel.
The beauty of pond waves alone is no small thing. By connecting nature to its main language – mathematics – we gain access to its control panel, allowing us to look at every detail, revealing all the secrets.
This article is republished from The Conversation, a non-profit, independent news organization that brings you reliable facts and analysis to help you make sense of our complex world. Written by: Nate Barlow, Rochester Institute of Technology
Read more:
Nate Barlow does not work for, consult with, own shares in, or receive funding from any company or organization that would benefit from this article this, and did not disclose any relevant connections beyond their academic appointment.