School maths teaching is stuck in the past. An adult returning to the school they attended as a child would only see major changes in their own experience.
Yes, in some schools they might see a room full of electronic tablets, or the teacher using a touch-sensitive interactive whiteboard. But if we zoom in on the details – the tasks that are being given to students to help them make sense of the material – things have hardly changed.
We have learned a lot in recent years about cognitive science – how our brains work and how people learn most effectively. This understanding could change what teachers do in classrooms. But the design of mathematics teaching materials, such as textbooks, benefited little from this knowledge.
Some of this information is counter-intuitive, so it is unlikely to be applied unless it is done deliberately. What learners prefer to experience, and what teachers think is most effective, is often not what will help the most.
For example, cognitive science tells us that practicing similar tasks together tends to produce less effective learning than mixing tasks that require different approaches.
In mathematics, a page of questions might involve practicing similar tasks, each of which requires adding fractions. Fractions, probability and equations may need to be brought together one after the other to mix things up.
Learners make more mistakes when doing mixed exercises, and are likely to feel frustrated. So it will probably be much easier for the teacher to group similar tasks together. But the mixed exercises give the learner important practice in deciding which method to use for each question. This means that more information is subsequently retained, leading to what is known as “desired difficulty”.
Cognitive science in action
We are just now beginning to apply these findings from cognitive science to design better teaching materials and to support teachers in their use. It makes sense to focus on school mathematics because mathematics is a compulsory subject that many people have difficulty learning.
Usually, school teaching materials are chosen by gut reactions. A department head looks at a new textbook scheme and, based on their experience, chooses which one they prefer. What else can they be expected to do? But even the best materials available are generally not designed with cognitive science principles like “desired difficulty” in mind.
My colleagues and I are researching educational design that applies principles from cognitive science to the teaching of mathematics, and are developing materials for schools. These materials are not designed to look easy, but to include “desired difficulty”.
They are not divided into individual lessons, as this puts pressure on the teacher to move on when the bell says, regardless of the students’ needs. Meeting the developing understanding and difficulties of students requires materials that are designed to scale, rather than conveniently fit into a double range of textbooks or a 40-minute class period.
Things change up
Adopting an approach guided by cognitive science means changing the way mathematical concepts are explained. For example, diagrams have always been a prominent feature of mathematics teaching, but are often used casually, based on the teacher’s personal preference. In textbooks they are very restricted, due to space constraints.
Often, similar diagrams are used in different subjects and for very different purposes, leading to confusion. For example, three connected circles as shown below can indicate division in a sum (the “part-whole model”) or product of prime factors.
These involve two very different operations, but are often depicted in the same diagram. Using the same type of diagram to represent opposite operations (addition and multiplication) confuses and confuses learners.
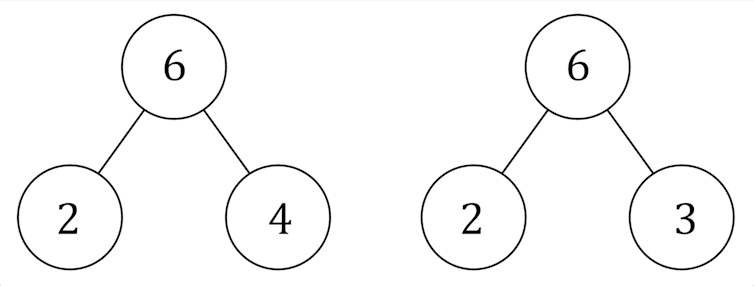
The “consistency principle” from cognitive science means avoiding illustrations when their disadvantages outweigh their benefits, and using illustrations and animations in a purposeful and consistent manner across topics.
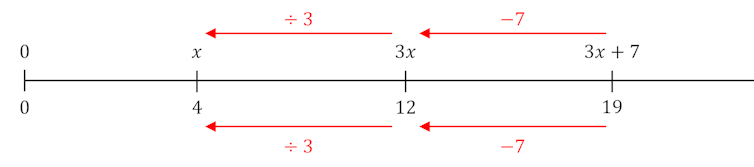
For example, number lines can be introduced at a young age and incorporated across many topic areas to provide coherence to students’ developing understanding of number. Number lines can be used to solve equations and also to represent probabilities, for example.
Unlike the circle diagrams above, the uses of the numbers shown below do not contradict each other but reinforce each other. In all cases, positions on the number line represent numbers, from zero to the left, increasing to the right.



There is a disturbing inequality in maths learning, with students from poorer backgrounds underachieving compared to their wealthier peers. There is a huge gender participation gap in maths, at A-level and beyond, with boys taking far more than girls.
Socio-economically advantaged families have always been able to buy their children out of trouble by using private tutors, but less privileged families cannot. Better quality instructional materials, based on insights from cognitive science, alleviate the impact on students who have traditionally been disadvantaged by gender, race or financial background in learning mathematics.
This article from The Conversation is republished under a Creative Commons license. Read the original article.


Colin Foster receives funding from Research England and the Economic and Social Research Council UKRI. He works with Loughborough University and is Director of the Loughborough University Mathematics Education Network.